Real-Time Symmetry-Preserving Deformation
In PG 2014. Other authors: Michael Wand, Klaus Hildebrandt, Pushmeet Kohli, Hans-Peter Seidel
Best Paper Award Honorable Mention
Problem statement
Our work is targeted at building an intelligent tool for 3D content creation, which is an important step for generating a wide variety of artistic data.

To create a new model, people normally start from a exist template shape. Such as these bottles, they look different, but all of the left three are derived from the rightmost neutral shape. That relates to human’s ability to abstract structures, and infer new variance in the meanwhile.

Structural organization is a very natural way for people to understand the target shape. So it is no coincidence that man-made shapes tend to have some prominent structure. One rigorous mathematical study of shape structure is symmetry group, which in 3D space basically means invariant to 3D transformations.
We adopt this notion in our work, and use symmetries as our structure representation. In the case of our content creation problem, we need an intelligent modeling tool that can understand the symmetry structure of the target shape.
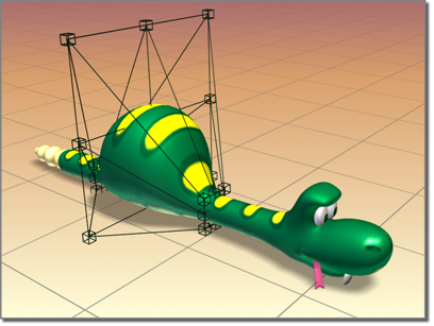
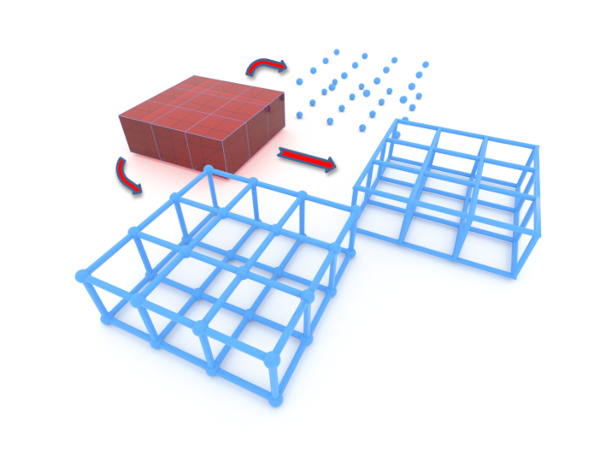
Modern modeling software has greatly improved productivity. For example, in this FFD application, a selected segment can be easily manipulated by very few control points. But for models with complex symmetry structure, how can we formulate symmetric editing?
Symmetry group: a primary introduction
Consider a surface $S$ in $R^{3}$ given by a two-manifold $M$ and an embedding $x:M \mapsto R^{3}$, we are interested in groups induced by Euclidean motions:
- A group $G$ is an algebraic structure consisting of a set of elements, which is closed under a binary operation (group action). In our discussion, $G$ consists of Euclidean motions.
- A Euclidean motion $g$ is an affine map whose linear part is an orthogonal transformation. Examples in 3D are translations, reflections, and rotations as well as any composition of these (Group Closure property).
- The orbit of an element $p$ on the surface $S$ is the set of elements in $S$ to which $p$ can be moved by the elements of $G$.
The set of Euclidean motions forms the Euclidean group $E(3)$ under composition of maps. We consider groups with respect to Euclidean motion, because this leads to useful invariants for man-made shapes.
For our experiments, we use standard triangle meshes as discretization of $S$ in $R^{3}$. In this case, $M$ is the surface mesh itself, while $x$ is the continuous and piece-wise linear map that maps every vertex to its positions in $R^{3}$.
Symmetry
An automorphism of $M$ is a map $\varphi:M \mapsto M$ that is a homeomorphism, i.e. is continuous, bijective and has a continuous inverse. Under the composition of maps, the set of automorphisms of $M$ forms a group that we denote by $\Psi(M)$. This concept is helpful in the following intrinsic formulation of our discussion.
Symmetries of $M$ relate to subgroups of $\Psi(M)$.
Any Euclidean motion $g$ can be composed with the embedding $x$, which results in a new map $g\circ x:M \mapsto R^{3}$. We are interested in surfaces and motions that the motion maps the surface onto itself.
Loosely speaking, a (Euclidean) symmetry of the embedded surface $(M,x)$ is a subgroup $G$ of $E(3)$ such that every $g\in G$ maps $x(M)$ to itself. More formally, we say that a subgroup $G\leq E(3)$ is a symmetry of $(M,x)$ if there is a subgroup $\Phi\leq\Psi(M)$ such that for every $g \in G$ there is a $\varphi\in\Phi$ such that
\[g\circ x=x\circ\varphi\]and the map $G\mapsto\Phi$ induced by this relation is a group isomorphism.
Partial symmetry
In addition to symmetries of the whole surface, we consider symmetries of parts of the surface and call them partial symmetries. This makes the concept more powerful as objects often only exhibit symmetries within local regions.
To define partial symmetries, we consider a submanifold $N$ of $M$, which need not be connected. Then, the restriction $x_{\large| N}$ of $x$ to $N$ is an embedding of $N$ in $R^{3}$; a symmetry $G$ of $(N,x_{\large| N})$ is a partial symmetry of $(M,x)$.
Note: It can take a whole year (or a whole life, e.g. some of my classmates :wink:) for a Math student to study higher algebra, but this short introduction is enough for understanding the background of our paper. If you think this discussion is boring: I am going to tease you with a beautiful dihedral group before ending this section:

Symmetry-Preserving Deformation
We describe deformations of the surface by variations of $x$. For this, we use a displacement map $u: M \mapsto R^{3}$. Then, the sum $x+u$ describes the deformed surface.
The resulting set of displacements forms a vector space. For triangle meshes, deformations are described by the displacements of the vertices. Then, the space of displacements equals $R^{3n}$, where $n$ is the number of vertices.
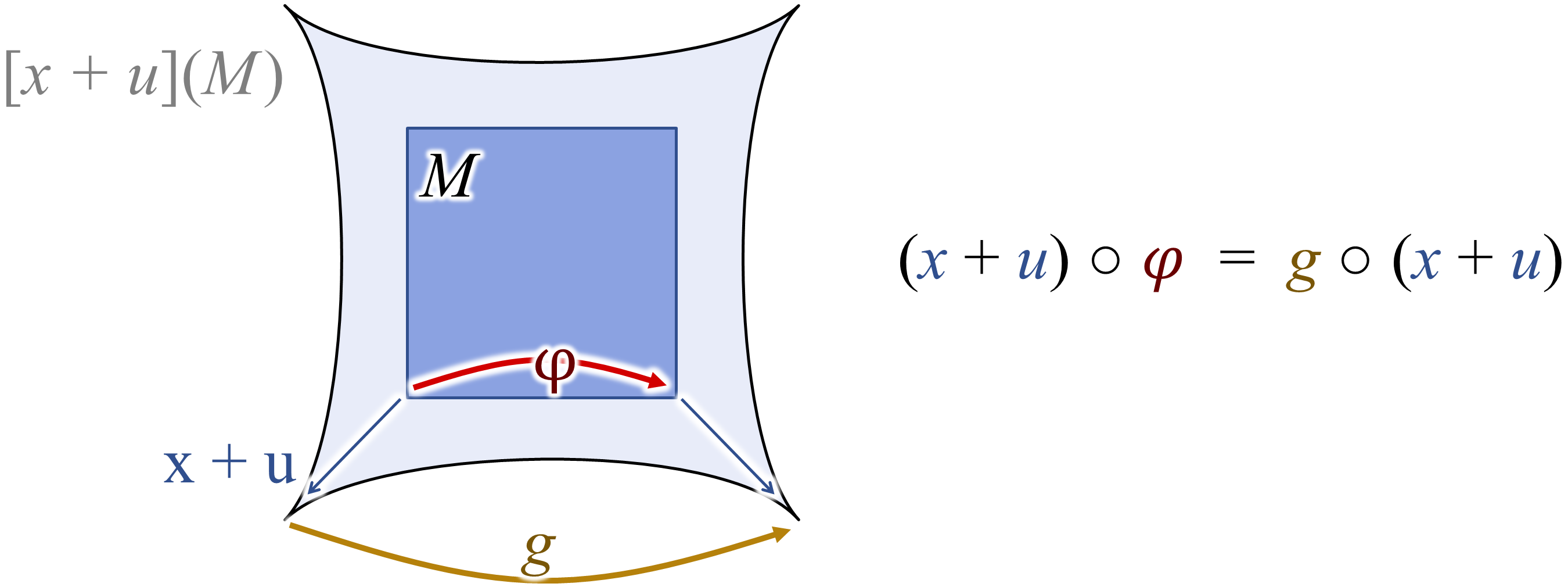
If we have a group $g$ that describes symmetries of the surface, then a displacement $u$ preserves the symmetry if
\[g\circ(x+u)=(x+u)\circ \varphi,\]where $\varphi$ is the automorphism induced by $g$. Figure~7 illustrates how this condition induces a symmetry-preserving deformation field.
The lemma of affine subspace
The basis of our surface modeling scheme is the observation that the set of all symmetry-preserving displacements forms a subspace of the vector space of all possible displacements (and thus the set of all possible deformations themselves form an affine space).
Given a symmetry group $G$ of a surface. The set of symmetry-preserving displacements forms a subspace of the vector space of all displacements.
The formal proof is very easy to follow, so please refer to the paper for the details.
The implication of this lemma
Knowing that the solution space is a subspace of discussion domain opens the door to subspace methods: now we are certain that the solutions to the problem live in a (usually) much small subspace, which can be found through a constructive algorithm, i.e. construct a set of basis that spans the target subspace. This is basically the essence of all classic and modern numerical optimization techniques that try to reduce the computation cost through factorization.
Subspace method based pipeline
If you follow the discussion to here, then you might already figure out how should our pipeline looks like:
- Generate a sparse set of symmetric samples on the surface,
- Construct a basis on those samples,
- Formulate an optimization objective given deformation constraints,
- Throw your favorite solver onto that objective,
- Lifting the displacements throughout the entire surface.
Anyway, there are some details worth to see in the following discussions.
Symmetric sampling
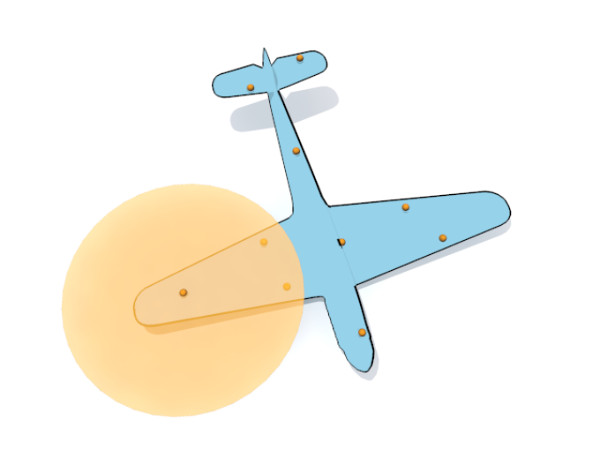
As optimization is only performed on that sparse set of points, it’s obvious that we want maximal sparsity. Given a fixed threshold $r$ as an input parameter to control density, we use Poisson disk (blue noise) sampling as the backbone:
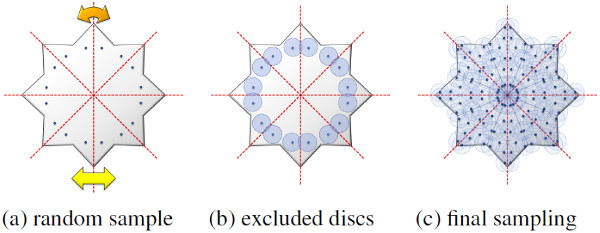
- First, a random point $p$ on the mesh $M$ is generated,
- To achieve symmetric editing, we analyze the (partial) symmetry structure $G$ and extract all the points that lie on the same orbit,
- Then we generate another random sample with a distance larger than $r$ to any of the already sampled points,
- Repeat the process until the entire domain is covered.
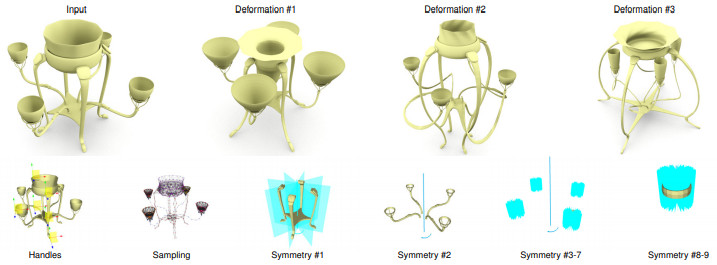
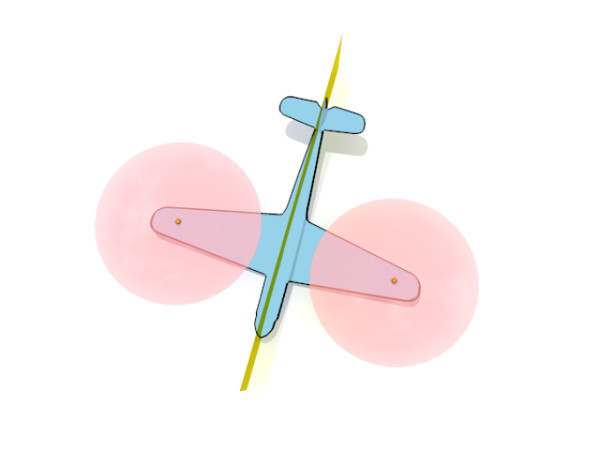
Here is a sampling example of a simple airplane model with two symmetries:
Nested and overlapping symmetries
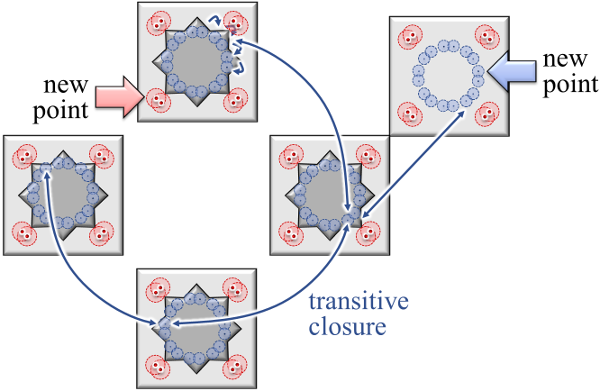
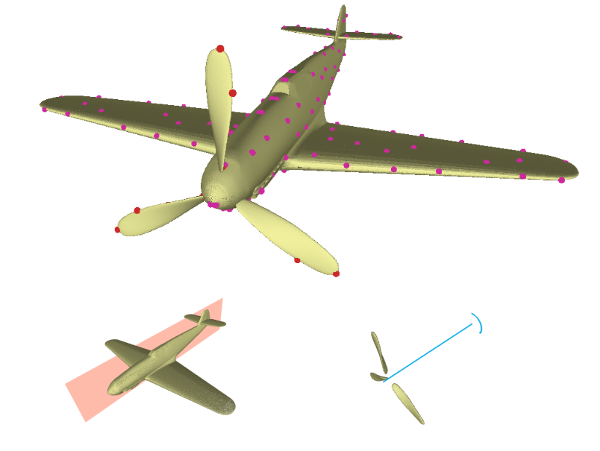
The same construction also works for nested and overlapping symmetry groups, where the transitive closure of the orbits is considered. The sampling algorithm generates these points by following and concatenating the local transformations during sampling. Please take a look at the teaser figure on the top of this page as an example, which has 9 symmetries including nesting and overlapping.
Basis construction

Let us first assume that the shape has only one reflective symmetry: during sampling, we collect the reflections that map every seed point to its counterpart. These seed points can be used to construct the space of symmetry-preserving displacements of the sampling.
Symmetry-preserving displacements of samples
Notice the following fact: whenever a point $p$ is transformed by a Euclidean motion $g(p)=O(p)+t$, a displacement $u$ of the point is transformed only by the orthogonal matrix $O$. Hence, we obtain a symmetry-preserving displacement of the sampling by displacing one vertex and propagating the displacement to the orbit of the point using only the orthogonal parts $O$ of the Euclidean motions $g$ (Fig~14).
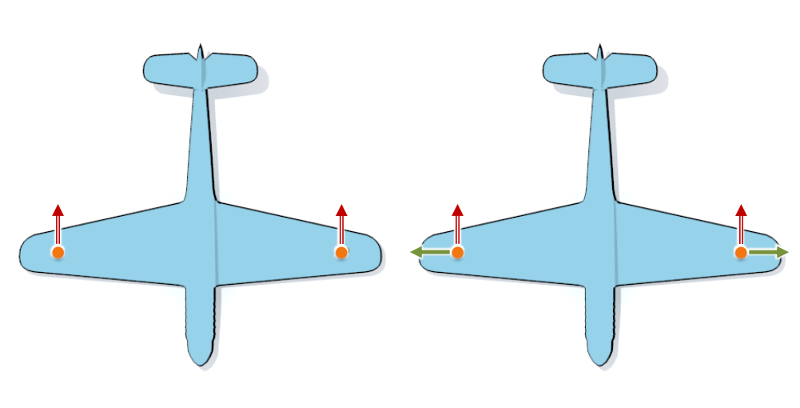
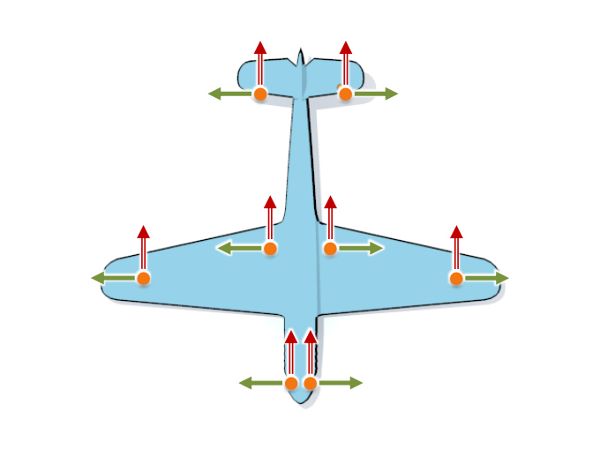
The orbit of any sample point $p$ has exactly three degrees of freedom in 3D (or two DoF for the airplane example in 2D). We apply the same procedure to select orthogonal unit displacements of $p$ into each of the three coordinate directions. To generate a basis of the space of symmetry-preserving displacements, we construct the three basis vectors for every seed point we placed during sampling.
Degenerate case
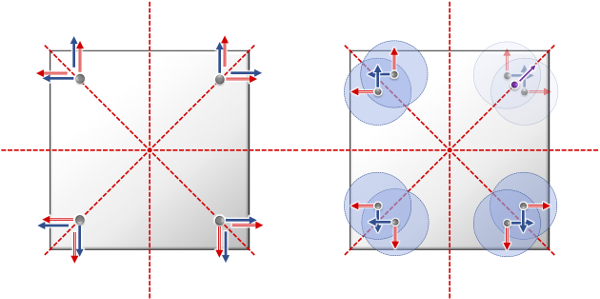
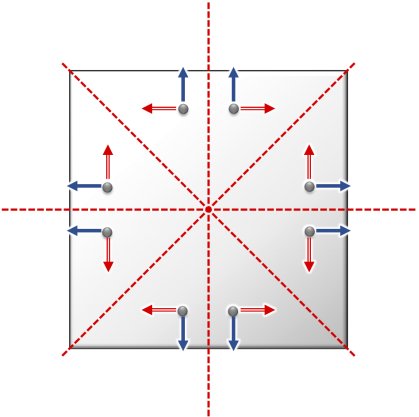
Case 1: A special case occurs if a sampling point is visited more than once but with different local frames $O_i$. This can happen on transformation-invariant sets, such as the diagonals in Fig~17 left: Here, we have orbits with four points from eight transformations, and each point has two different frames, differing by a reflection.
The correct solution is obtained by reducing the dimension of the basis to those vectors $v$ for which $O_i v = O_j v$ for all $i,j$, which yields a linear system of equations. Notice that due to the random sampling, this is rarely encountered in practice. In relevant cases, we can perform an SVD reduction of the null space to remove spurious degrees of freedom.
Case 2: If points do not perfectly overlap but only come close (which is still usually close to transformation-invariant sets, see Fig~10 (c)), we do not need to take special measures — the contributions of the basis functions cancel out exactly; we only obtain some overhead due to too dense sampling. The overhead is small as it only occurs at transformation-invariant sets of measure zero (reflection planes, rotation centers, Fig~17 right).
Lifting the displacements
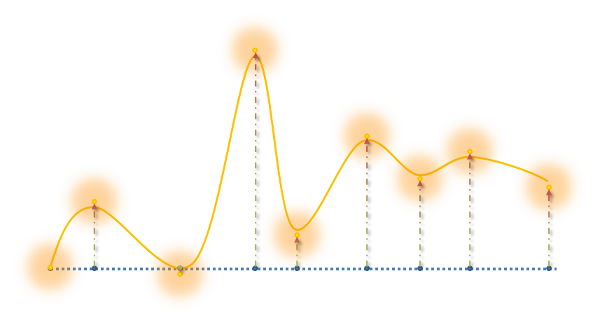
To propagate a displacement of the sampling to a displacement of the surface, we compute for each basis vector $\bar{b}$ of the space of symmetry-preserving displacements of the sampling a corresponding displacement vector $b$ of the mesh. Then, the displacement $\bar{u}= \sum_{i} q * \bar{b}$ of the sampling (orange points) is lifted to the displacement $u=\sum_{i} q * b$ of the mesh (solid line/curve).
A displacement of a sampling point should only affect the displacement of the mesh vertices in a local neighborhood. We use Gaussian functions with standard deviation equal to the sampling density around every sample point to assign influence weights to the mesh vertices. Due to the compact support property weight $w_{kl}$ is sparse.
The basis vectors $b_{i}$ are given by a partition-of-unity:
\[b_{i}(v_{k})=\frac{1}{\sum_{l}w_{kl}}\sum_{l}w_{kl}\bar{b}_{i}(\bar{v}_{l}).\]Notice: the basis $b_{i}$ can be precomputed such that the Gaussians need not be evaluated in the interactive editing phase, which leads to much faster real-time solver.
Real-time Editing
Once the subspace of symmetry-preserving displacements has been constructed, any deformation-based editing scheme could be used to produce symmetry-preserving deformations. Only the set of feasible displacements needs to be restricted to the subspace.
However, as the meshes can be highly resolved, the computation of a deformation can be expensive. To be able to compute deformations of the surface in real-time, we restrict to low-frequency deformations that are liftings of displacements of the sampling.
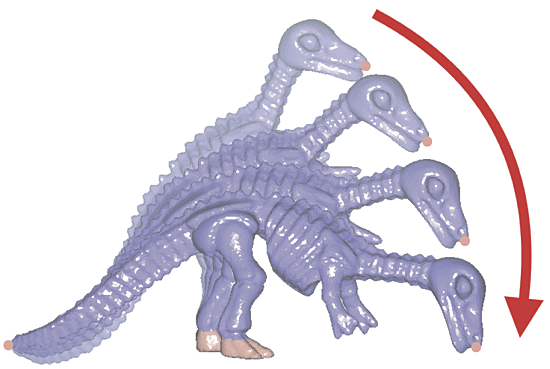
To compute the displacements of the sampling, we use an iterative co-rotated Laplace editing approach. The reasons for choosing this are approach are:
- We obtain a non-linear editing scheme that allows for large deformations,
- We only need minimal additional structure to compute the deformations. Namely, we need a Laplace matrix for the sampling and a list of neighbors for each vertex.
Laplace editing
The basis of the non-linear iterative co-rotated Laplace editing is the linear Laplace editing: The deformation is computed by solving a quadratic minimization problem. The objective functional combines two quadratic functionals:
- One measures the deviation of the so-called Laplace coordinate,
- The other measures the deviation (in a least-squares sense) from user-specified constraints, such as target handle location, colinear/coplanar, etc.
We denote by $\bar{x}$ the vector listing the coordinates of the sample points and by $\bar{u}$ the displacement of the sampling points. The vector of Laplace coordinates is $\delta=L\bar{x}$ and the first quadratic functional is
\[E_{L}(\bar{u})=\left\Vert L(\bar{x}+\bar{u})-\delta\right\Vert ^{2}.\]In our implementation, the user can select handle regions in the sampling and assign desired positions to the selected sample points by rotating and translating the handles in space (see accompanying video). The corresponding least-squares functional is
\[E_{C}(\bar{u})=\left\Vert A(\bar{u})-a\right\Vert ^{2},\]where $a$ lists the desired displacements of all vertices in the handle regions. The matrix $A$ is rectangular and has only one non-zero entry per row, which takes the value 1.
The resulting deformation is given by the displacement that minimizes
\[E(\bar{u})=E_{L}(\bar{u})+\alpha E_{C}(\bar{u})\]among all symmetry-preserving displacements. The hyper-parameter $\alpha \in R_{+}$ controls how strongly the surface is pulled towards the user-specified handle positions.
Iterative co-rotated Laplace editing

A limitation of Laplace editing is that deformations that include larger rotational components lead to visually observable artifacts in the deformed surface. Therefore, we use a non-linear variant obtained by iteratively applying Laplace editing.
Some notes: The Laplace coordinate can be interpreted as a vector field on the sampling specifying a 3-dimensional vector $\delta_{i}$ for every vertex. The Laplace coordinate is related to the discrete mean curvature normal and every $\delta_{i}$ should point into the direction of the surface normal at the corresponding sample point. The rotation matrix can be computed using SVD.
The null-space method
To solve the quadratic program, we use the null-space method, which is an effective method to reduce computation cost in case of a highly constrained optimization problem.
Elementary constraint optimization

Let $L$ be the objective matrix, and $H$ be the matrix derived from hard constraints (such as symmetry constraints), from numerical optimization we know that the problem is equivalent to solving a linear system looks like Fig~20 left.
You can imagine that the computation cost is rather huge for problems with lots of variables (3 times of the number of samples) and constants (usually we need constraints for keeping the object looks good, such as points stay on the same plane during editing).
Null-space projection
The key idea of the null-space method is to project variables onto the null-space (aka kernel in linear algebra) of constraint matrix $H$:
Rank–nullity theorem: Let $N$ be rectangular and $V$ is the variable domain, $N$ is the null-space induced by $H$, $\iff$ $dim(H) + dim(N) = dim(V)$.
The null-space method states that when $N$ is found, two linear systems in Fig~20 have the same solution set. Notice that the scale of the linear system on the right is strictly smaller than the one on the left, and usually has a much smaller scale in practice, which implies much lower computation cost. Please refer to Numerical Optimization, Chapter 16.2 for a more canonical discussion.
Note: it’s very easy to see that null-space method is especially effective when the rank of $H$ is large, which is exactly our case since the target object is under a large number of symmetric constraints. This is very contrary to our general intuition: more constraints normally means a larger and more expensive linear system to solve in standard methods; while in the null-space method, more constraints will reduce more degrees of freedom, which means less expensive computation.

In the example above:
- For a simple airplane model, the problem scale reduces to less than one third after applying the null-space method,
- For a more complex model with more symmetry structure, the problem scale is reduced drastically.
Construct the null-space
So far, the method sounds promising, but why is the null-space method less well-known comparing to the standard constraint optimization methods? Well, the problem is that there is no canonical way to directly construct a basis for the null-space in general case, and sometimes the null-space is even harder to find than solving the original problem itself.
In this project, we studied the numerical structure of symmetry constraints, and found a canonical way to construct the null-space in this special case. The algebraic proof is not shown in the paper due to page limitation, so I will write it down here for further reference. This is one of the main contributions of our work.
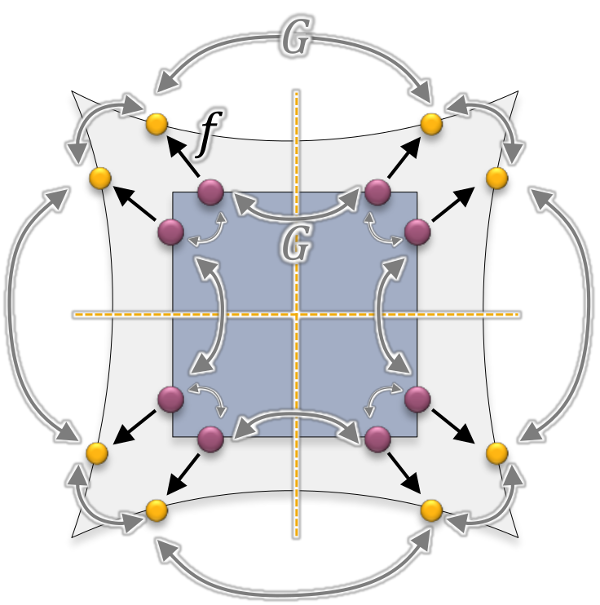
Take a look at this simple case where the dark square is stretched to a shape in light gray. Here we only consider one orbit in its symmetry structure $G$ (group actions shown in gray) for clarity. As discussion in the section of Symmetry-preserving displacements of samples, we optimize for displacements $U = [u_1;u_2; …;u_n]$ of each sample (originated from violet dots) under the deformation field $f$ (shown in black).
We can easily formulate the symmetry constraint as $HU=0$, where matrix $H$ has the following structure (Hint: $I$ is the identity matrix in $R^3$ and $O_{1..n}$ are orthogonal transformations (full-rank matrices), so $Iu_1 - O_2u_2 \iff u_1 = O_2u_2$ for the second row):
\[H = \begin{bmatrix} I \\ I & -O_2 \\ I & & -O_3 \\ I & & & -O_4 \\ \vdots & & & & \ddots \\ I & & & & & -O_n \\ \end{bmatrix}, \\ N = \begin{bmatrix} I & O_2 & O_3 & O_4 & \cdots & O_n \end{bmatrix}\]To proof $N$ is the null-space matrix of $H$, we need to show $V=[H;N]$ is full-rank ($dim(V)=3n$).
Proof.
-
Subtract the first row of $H$ from every other row, we immediately know: $rank(H)=3(n-1)$,
\[H_1 = \begin{bmatrix} 0 \\ & -O_2 \\ & & -O_3 \\ & & & -O_4 \\ & & & & \ddots \\ & & & & & -O_n \\ \end{bmatrix}\] -
It’s obvious that $rank(N)=3$. Now add all the rows of $H_1$ to $N$:
\[N_1 = \begin{bmatrix} I & 0 & 0 & 0 & \cdots & 0 \end{bmatrix}\] -
It’s obvious that $rank(H_1;N_1) = 3n$, so $rank([H;N])=3n$.
Q.E.D.
Summary and other acceleration techniques
Let $N$ be the rectangular matrix whose columns are the basis vectors of the space of symmetry-preserving displacements of the sampling, and let $q$ be the vector of coordinates with respect to the basis. To compute the minimizer of the energy functional in the space spanned by $N$, we have to solve the linear system
\[N^{T}(L^{T}L+\alpha A^{T}A)Nq=N^{T}(\alpha A^{T}a+L^{T}(\delta-L\bar{x}% )).\]Note: $L^{T}L+\alpha A^{T}A$ is a formulation of soft constraints, where $\alpha$ is the Lagrange multiplier.
- Since the symmetric, positive definite matrix $N^{T}(L^{T}L+\alpha A^{T}A)N$ only changes when new handle regions are selected or the weight $\alpha$ is modified, it is efficient to compute a Cholesky factorization of this matrix and to re-use it for solving the minimization problems.
- In addition, using a factorization speeds up the iterative co-rotated Laplace editing.
- We also transfer the computation to GPU through cuBLAS.
Experiments
Since we are talking about real-time editing, here I only show some editing videos.
Conclusion
We present a method for real-time symmetry-preserving shape modeling. The basis of the scheme is a construction of spaces consisting of low-frequency deformations that preserve the symmetry. Within these low-dimensional spaces, we apply a non-linear deformation-based editing scheme.
We demonstrate real-time deformations that preserve the symmetries exactly and support large deformations. The method is much easier to implement than previous optimization-based methods and significantly faster.
Appendix: Abstract
In this paper, we address the problem of structure-aware shape deformation: We specifically consider deformations that preserve symmetries of the shape being edited. While this is an elegant approach for obtaining plausible shape variations from minimal assumptions, a straightforward optimization is numerically expensive and poorly conditioned. Our paper introduces an explicit construction of bases of linear spaces of shape deformations that exactly preserve symmetries for any user-defined level of detail. This permits the construction of low-dimensional spaces of low-frequency deformations that preserve the symmetries. We obtain substantial speed-ups over alternative approaches for symmetry-preserving shape editing due to (i) the sub-space approach, which permits low-res editing, (ii) the removal of redundant, symmetric information, and (iii) the simplification of the numerical formulation due to hard-coded symmetry preservation. We demonstrate the utility in practice by applying our framework to symmetry-preserving co-rotated iterative Laplace surface editing of models with complex symmetry structure, including partial and nested symmetry.
Appendix: Related work
Before going into the details of our construction, we would like to list some closely related work back in 2014.
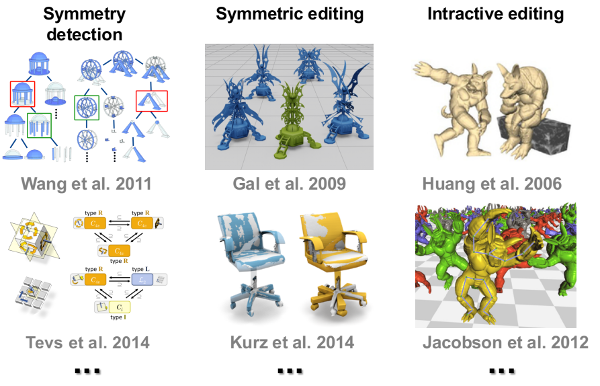
Symmetry detection
The first element is symmetry detection, which provides the input to our pipeline. Wang et al. 2011 organized symmetries in a hierarchical way for better understanding very complex shape composition. Symmetry groups are studied in Tevs et al. 2014, which follows a very detailed classification philosophy (our work uses the results provided by this work).
Symmetric editing
The seminal work from Gal et al. 2009 uses a feature-based description of shape structure, and can keep certain Euclidean invariance through optimization. Another work by Kurz et al. 2014 Builds symmetric mapping from a template shape to the target scan data.
Interactive editing
For achieving interactive editing, one line of research resort to subspace method. The method restricts the deformation on a predetermined subset of variables, then propagates the motion to the entire mesh. For example, Huang et al. 2006 builds a coarse control mesh around the original mesh; while Jacobson et al. 2012’s work, control points can be disconnected.
Our goal is to combine all these ingredients, and propose a generic editing framework.
